Cycles of polynomial maps

This page is about an algorithm for computing the exact n-cycles of some polynomials maps.

Introduction

Consider a one-dimensional map,
x → f (x),
where f(x) is some polynomial function.
If we iterate the map many time, we would have an iteration sequence:
xk+1 = f (xk).
Occasionally, this sequence would go back to some previous value after a few iterations, and afterwards, it simply repeats itself. This is what we call a cycle. The mathematical problem we wish to figure out is that when does such a cycle happen.

Cycles and fixed points

An n-cycle is a sequence x0, x1, ... xn, such that
xn = x0.
Here, n has to be the smallest positive integer that satisfies the relation.
After the first cycle, the pattern would repeat itself, and we would have
x n+k = xk
for k.
Particularly, a 1-cycle is called a fixed point, that is, the solution of
f (x0) = x0.
Any cycle point xk in the n-cycle of f is also be a fixed point of the iterated map fn, (which is called the nth iterate of f) for
xn+k = fn(xk ) = xk.
However, a fixed point of fn (n > 1) is not necessarily a n-cycle point. For example, a fixed point of f is also a fixed point of its nth iterate, but is not qualified as a ncycle point.

Stable cycles

A cycle can be stable or unstable. In a stable cycle, a small deviation from the exact cycle point x0 gets reduced in magnitude after n iterations, such that xn becomes closer to the exact cycle point than x0. In other words, a stable cycle is attractive in the neighborhood of its cycle points.
A stable cycle is generally more meaningful than an unstable one. If we start the iteration from a random x0 it will be converged only to a stable cycle.
We further note that if xk are complex numbers, a cycle always exists, for we can always find complex roots of the algebraic equation fn(x) = x.

Statement of the problem

Now let us say the map f depends on a parameter r. For example, in the logistic map,
f (x) ≡ r x (1 − x).
Both the cycle points and the cycle stability of a cycle depend on the parameter r. The problem we are trying to tackle here is to determine the r values that allow stable n-cycles.

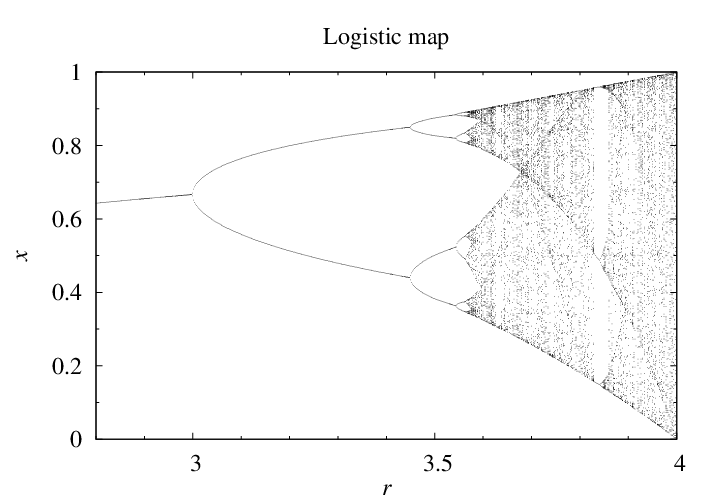
Bifurcation diagram

Stable cycles can be visualized in a bifurcation diagram as shown below (for the logistic map). Starting from a random x0 (0.1 here), the final xk points after a large number of iterations are plotted against the value of the parameter r. Obviously, all xk points shown in the plot belong to a stable or attractive cycle.
bifurcation diagram of the logistic map

Onset and bifurcation points

Our purpose is to determine the r values at which stable n-cycles exist. As we usually are interested in real r and xk, the r values for stable cycles are arranged as windows on the real axis. For example, as shown in the above figure (logistic map), the stable 2-cycle exists in the window (3, 1 + √6) = (3, 3.449...). We shall call the two bounds as the onset and bifurcation points of the cycle.
For a polynomial map, the r values at the onset and bifurcation points are algebraic numbers, i.e., they are zeros of some polynomials of integral coefficients. Our problem is, therefore, to find one polynomial that encompasses all onset r values as the zeros, and the other polynomial for all bifurcation r values.

Derivative condition

The onset and bifurcation points of the n-cycle can be determined from the derivative of the composite map [ f n(x) ]′ = [ f (⋯( f (x)⋯) ]′ . Since a stable cycle must reduce the magnitude of x after n successive iterations, the magnitude of this derivative must be 1.0 at the two critical points. More precisely, +1 and −1 are assigned to the onset and bifurcation points, respectively. Thus by the chain rule, we have
f ′(x1) ⋯ f ′(xn) = ±1,
at the onset (+1) and bifurcation (−1) points.
The n equations, xk+1 = f (xk) (with xn = x0), along with the derivative condition, furnish n + 1 equations. Thus, we can eliminate the n variables xk and obtain the desired equation of r.

Individual maps

Individual maps has separate pages. The onset and bifurcation polynomials can be found there.

Programs

For convenience, we list a few main programs here.
Program Description
log.ma A Mathematica script for the cycle polynomials of the logistic map
cub.ma A Mathematica script for the cycle polynomials of the cubic map.
hen.ma A Mathematica script for the cycle polynomials of the Hénon map.
lsfit.ma A specialized Mathematica script that interpolates a polynomial from a list of values, generated by log.ma or cub.ma after a parallel or unfinished run see here.
mkinterp.py A Python script that generates a specialized Mathematica script, which interpolates a polynomial from a list of values. For logistic and cubic map, use the faster lsfit.ma in the above instead. Reserved for the Hénon map.
mknsolv.py A Python script that generates a specialized Mathematica script, which numerically solves zeros of the polynomial r-cycles (the output of lsfit.ma.)

A note on the Mathematica scripts (.ma files)

The “.ma” file, listed here, are plain-text Mathematica scripts. The extension “.ma” is arbitrary, it can also be “.txt”. Unlike the Mathematica notebooks (.nb files), they do not contain formatting information and can be edited by any text editor (e.g., Notepad, Vim, or Emacs) instead of the default Mathematica GUI editor. To run such a script (say myprog.ma), type in the command-line
math < myprog.ma argument1 argument2 ...
Here, math (or math.exe in Windows) is the file name of Mathematica's main command-line driver, which should be installed under same directory as the GUI interface mathematica (or Mathematica.exe in Windows). If this directory is not added in the environment variable PATH, the full path to math should be used in the above command.

References

General

Primary reference

Last updated on April 2nd, 2014.