Cycles of the antisymmetric cubic map
Introduction
The cubic map is defined as:
xk+1
= f (xk)
≡ r xk − xk3.
This map is also related to the one studied by Brown (Brown 1984a,b):
qk+1
= a qk3
+ (1 − a) qk.
The map is quite similar to the logistic map;
and the basic concepts about cycles are applicable here.
A distinct feature of the map is that it has an odd parity:
f (−x) = −f (x),
which gives the map several unique properties.
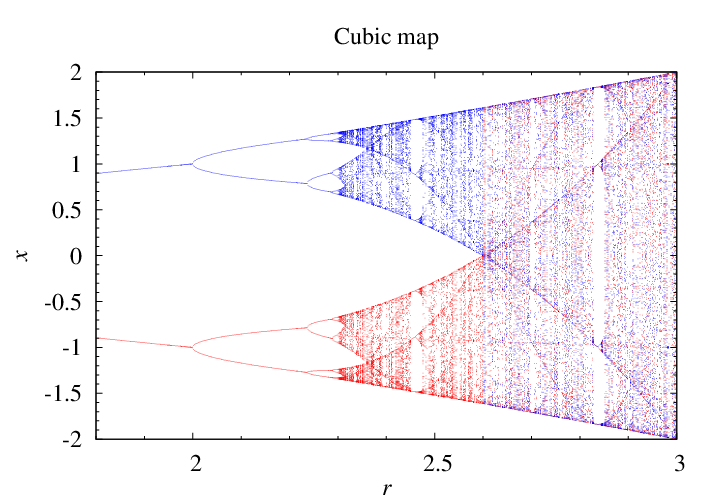
Bifurcation diagram
The bifurcation diagram is shown in below.
Globally, it is quite similar to the case of the
logistic map.
However, it contains two branches (shown in blue and red) due to the odd parity of the map.
Starting from different
x0,
say +0.1 and −0.1,
the sequence will be converged to different final values.
Thus, the window
(2, √5) = (2, 2.235...)
represents 2-cycles, not 4-cycles.

Mandelbrot set
Like the logistic case,
the method is applicable to complex n-cycles.
The regions of complex R values
that allow stable complex n-cycles
are plotted below. The figure is the Mandelbrot set of the cubic map.
n-cycle data
We list the polynomials involved in the n-cycles below.
The numerical zeros are appended at the end of each file.
For the general boundary polynomial of
n-cycles, we defined
X = (r − x12)
⋯
(r − xn2),
and list the polynomial of
r
versus
X
(as shown as “r-X”).
You can right-click each item and save.
| n | Onset | Bifurcation | General |
|---|---|---|---|
| 1 | eq. | eq. | r-X |
| 2 | eq. | eq. | r-X |
| 3 | eq. | eq. | r-X |
| 4 | eq. | eq. | r-X |
| 5 | eq. | eq. | r-X |
| 6 | eq. | eq. | r-X |
| 7 | eq. | eq. | r-X |
| 8 | eq. | eq. | |
| 9 | eq. (.zip file) | eq. (.zip file) |
Programs
| Program | Description |
|---|---|
| cub.ma |
A self-contained Mathematica script that computes
the onset and bifurcation polynomials
of r
for the n-cycles.
For the onset polynomial of the 7-cycles, type
math < cub.ma 7 a
The output would be
cr7a.txt.
For the bifurcation polynomial of the 6-cycles, type
math < cub.ma 6 b
The output would be
cr6b.txt.
For the general boundary polynomial of the 5-cycles, type
math < cub.ma 5 X
The output would be
cr5X.txt.
A variant can be accessed through
“X”
instead of
“Y”.
For the complex branching polynomial of the intersection of the 3-cycles and 21-cycles, type
math < cub.ma 3 x 21
The output would be
cr3x21.txt.
|
| lsfit.ma | A Mathematica script that computes a polynomial from interpolating a list of r values. This is used in parallel runs, see here for details. |
|
|
|
| mknsolv.py | A Python script that generates a Mathematica script, which numerically solves the polynomial equation of r. |
| mkgb.py | (Slow) A Python script that generates a
Magma
script,
which solves the boundary polynomial
by constructing a Gröbner basis.
For example, to compute the bifurcation polynomial
of the 5-cycle for the cubic logistic map, type
python mkgb.py 5 b > c5b.magma
Then call magma
magma < c5b.magma
To compute the onset polynomial, type
python mkgb.py -c 5 a > c5a.magma
magma < c5a.magma |
| cub2.ma | A Mathematica script that computes a transformed cubic map, which encompasses both n-cycle and n-half-cycle polynomials. The usage is similar to cub.ma. |
Click here to see how to use the Mathematica scripts
.ma files.
References
Primary reference
- Cheng Zhang, Cycles of the logistic map, International Journal of Bifurcation and Chaos 24 (2014) 1450005; also, an earlier preprint: arXiv:1204.0546, 2012.
General information
- Steven H. Strogatz, Nonlinear Dynamics And Chaos: With Applications To Physics, Biology, Chemistry, And Engineering" Westview Press, 2001
- Bailin Hao, Elementary Symbolic Dynamics and Chaos in Dissipative Systems, World Scientific, 1989
A related cubic map
- A. Brown, Solutions of period three for a non-linear difference equation J. Austral. Math. Soc. Ser. B 25 (1984), 451-462.
- A. Brown, Solutions of period four for a non-linear difference equation J.. Austral Math. Soc. Ser. B 26 (1984), 146-164.
Last updated on April 2nd, 2014.
